Nos Exercícios 1-12, associe a equação com a superfície que ela define. Além disso, identifique cada superfície pelo tipo (paraboloide, elipsoide etc.) As superfícies vão de a-l
4.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Este exercício visa que, com base na equação dada:
Identificar a superfície por tipo. Então, vamos reescrever a equação dada em uma forma que possamos identificar facilmente. A equação quadrática tal que os coeficientes de são diferentes, um dos coeficientes é negativo e dois dos coeficientes são positivos, nenhum outro termo quadrático aparece e nenhum termo constante aparece, corresponde a um cone.
Nossa equação pode ser reescrita como:
Então o coeficiente de é negativo e os coeficiente de e são positivos. Assim, assumimos que a equação dada corresponde a um cone com o eixo como eixo de simetria (porque o coeficiente de é negativo).
O cone elíptico com o eixo como eixo de simetria tem a seguinte equação:
Passo 2
A equação dada pode ser expressa da seguinte forma:
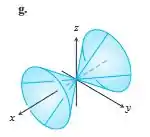
Portanto, notamos que nossa equação tem a forma dada acima com , e . Considerando as superfícies dadas, notamos dois cones elípticos. O cone elíptico na parte (h) tem o eixo y como eixo de simetria, enquanto o cone elíptico na parte (g) tem o eixo x como eixo de simetria. Assim, podemos concluir que a equação dada descreve o cone elíptico dado na parte (g).
Resposta
Respondido acima!