Nos Exercícios 17-24, descreva os conjuntos de pontos no espaço cujas coordenadas satisfazem as desigualdades ou combinações de equações e desigualdades fornecidas.
Passo 1
Olá pessoal, antes de iniciarmos este exercício iremos relembrar um pouco a teoria.
Os três eixos coordenados determinam três planos coordenados, de acordo com a Figura:
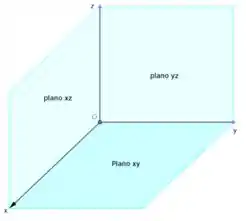
O plano contém os eixos e , o plano contém os eixos e e o plano contém os eixos e
Passo 2
Se o centro da esfera é a origem , a equação dela é:
Sendo assim, a equação:
É uma esfera com raio 1.
Para o item a., temos a equação:
Então é uma esfera com raio 1 centrada na origem.
E para o item b.:
São todos os pontos a mais de 1 unidade da origem.
Tchau pessoal, até mais!
Resposta
- A esfera de centrada na origem.
- Todos os pontos a mais de 1 unidade da origem.