Nos exercícios 11-14, use os valores tabulados do integrando para estimar a integral com (a) a regra do trapézio e (b) a regra de Simpson com passos. Arredonde suas respostas para cinco casas decimais. Depois (c) determine o valor exato da integral e o erro na aproximação para ou , como for apropriado.
11.
Passo 1
Falaaaa... beleza?
Nessa questão vamos precisar da regra do trapézio, que para fazer a aproximação para usamos:
Também da regra de Simpson:
Os são os valores de nos pontos da partição
Onde .
Passo 2
Ohhh... repara que:
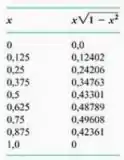
Que é exatamente o intervalo dos valores que são dados na tabela... Então já temos os valores de tudinho. Só precisamos jogar nas fórmulas.
a) Para a regra do trapézio:
Lembrando que ele pediu com cinco casas decimais, ok?
Passo 3
b) E agora usando a regra de Simpson:
Passo 4
Agora é o grosso da questão. Bora resolver essa integral na raça.
c) Usando o método da substituição simples, chamamos:
Para os limites de integração:
Então ficamos com:
Então temos que:
Só falta agora calcular o erro que é só a gente subtrair o valor exato do valor da aproximação.
Para a regra do trapézio:
Para a regra de Simpson:
Ufa... acabamos.
Resposta
a)
b)
c)