Expresse a integral iterada como uma integral dupla em coordenadas polares.
Passo 1
Olá galera! Nos deram este desafio de expressar a integral iterada dada em coordenadas cartesianas em coordenadas polares. A dica é observar os intervalos de integração e a variável de integração correspondente para encontrar a região no plano XOY. Esboçando a região teremos como obter a relação entre as coordenadas cartesianas e polares. Temos os seguintes intervalos: e . Assim, a nossa região é
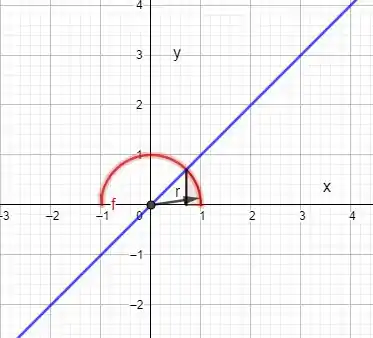
Passo 2
Vamos nesta jornada! No esboço da região procurada podemos encontrar sem dificuldades o intervalo de variação do ângulo , e que nesse caso é,
Passo 3
Galera, a nossa tarefa agora é determinar o intervalo onde o raio que gera esta região se situa. Como e chamando o raio menor que descreve a curva preta de , isto implica que . Continuando teremos,
Galera, já estamos na posse do raio menor, e do raio maior, , então o intervalo procurado é,
Assim, a nossa resposta final é