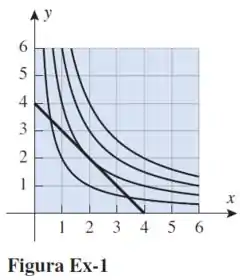
A figura a seguir mostra o gráfico da reta e as curvas de nível de altura para a função .
(a) Use a figura para encontrar o valor máximo da função sujeita à restrição e explique seu raciocínio.
(b) Como podemos dizer, a partir da figura, que a resposta em (a) não é o valor mínimo de sujeita à restrição?
(c) Use multiplicadores de Lagrange para verificar seu trabalho.
Passo 1
Fala galera, vamos começar mais uma questão.
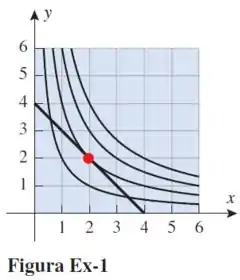
Letra (a) pede para usar a figura para encontrar o valor máximo da função sujeita à restrição e pede para explicar o nosso raciocínio.
A figura apresenta as curvas sujeiras à restrição e a reta da função. O ponto onde essa reta tangencia alguma dessas curvas é considerado o valor máximo da função, assim nosso valor máximo ocorrem no ponto (2,2), ponto em vermelho, e corresponde ao valor de 4.
Passo 2
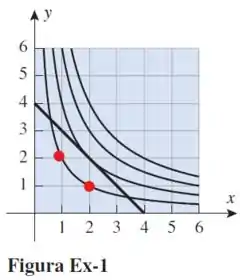
Agora vamos para a letra (b) Como podemos dizer, analisando a figura, que a resposta em (a) não é o valor mínimo de sujeita à restrição?
Observando as curvas, reparem que a primeira curva passa pelos pontos (2,1) e (1,2), esses são nossos menores pontos, eles que resultam em que é o nosso valor mínimo.
Passo 3
Letra (c) Vamos aos cálculos usando os multiplicadores de Lagrange.
Fazendo as substituições em:
O que equivale a:
Igualando
Substituindo em , temos:
Logo:
Assim chegamos que os valores máximos igual a no ponto (.