Se C for o círculo unitário orientado no sentido anti-horário e F(x, y) = xi + yj, então
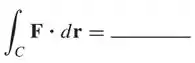
Passo 1
Olha só como nós vamos resolver essa questão!
Primeiro é importante entender o comando da questão que diz que nós temos uma curva de um cículo C orientado pela equação no sentido anti-horário, ou seja vai de a 0. A partir disso, temos de calcular sabendo que F(x, y) = xi + yj .
Passo 2
Vamos começar a manipular as equações, isso pois a integral dada pode ser escrita de outra forma:
Isso facilita para obtermos os termos restantes, os componente de F são os termos que acompanham “i” e “j” na equação F(x, y) = xi + yj , logo, F(x,y)
Para descobrirmos o dx e dy temos que obter as equações paramétricas, ou seja, representar por uma única variável a equação do cículo.
E depois basta deriva x e y:
Passo 3
E por fim, se substituirmos esses valores na integral (1), temos:
Facilmente resolvendo a integral, obtemos o valor zerado.