Se a força viscosa no Problema 3 é não linear, um modelo possível seria fornecido pela equação diferencial
Redesenhe o campo de direção na Figura 1.14 para incorporar essa dependência υ³. Esboce as soluções com condições iniciais υ(0) = 0, 1, 2, 3. Qual é a velocidade terminal neste caso?
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
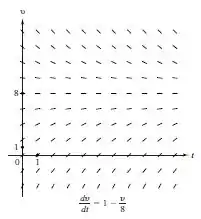
Passo 2
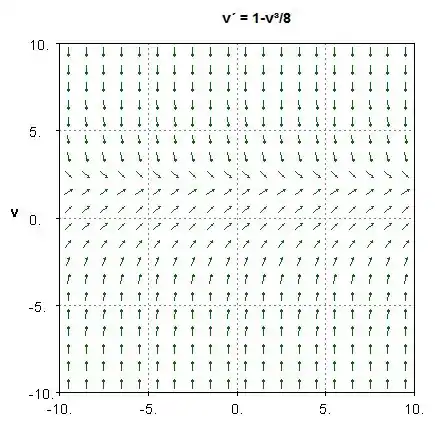
Considere o gráfico de acima.
Quando a razão de v para 8 é a mesma, o gráfico converge para uma linha singular. Da mesma forma, o gráfico de v³, mas agora para obter v³ = 8V deve ser igual a 2. Nota: Como a função é linear e homogênea, pode-se resolver a divergência definindo v′(t)=0 e prossiga para resolver para v(t).
Passo 3
Considere que não temos a interface gráfica para representar graficamente o campo de direção. Substitua os diferentes valores de v na EDO para resolver a inclinação v′(t) em cada valor.
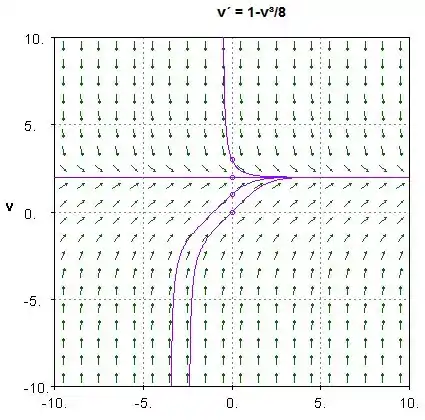
Podemos prosseguir para desenhar as curvas de solução que se curvam em direção à linha de convergência v=2. Esses pontos cruzarão os pontos dados (v,t) e seguirão a direção da inclinação correspondente. Como podemos ver a EDO tem convergência sobre o intervalo
(−∞,2]∪[2.∞)