A função é periódica se existir um número positivo (período da função) tal, que para todos os valores de , pertencentes ao campo de existência da função .
Determinar quais das funções abaixo enumeradas são periódicas e achar, para as funções periódicas, o período de seus :
- ;
- ;
- ;
- ;
Passo 1
Analisando o gráfico da função, temos:
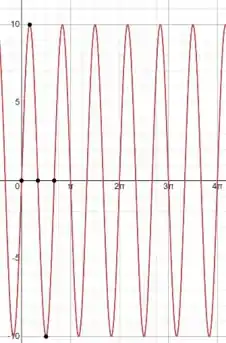
Assim, podemos ver que a cada , a função volta a repetir seus valores. Então:
Passo 2
Analisando o gráfico da função:
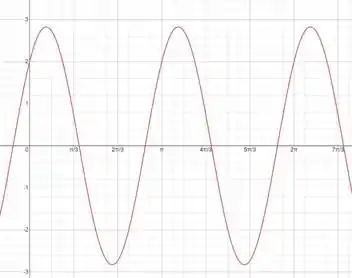
Adotando , vemos que a função volta a repetir em , ou seja, . Então:
Passo 3
Analisando o gráfico da função:
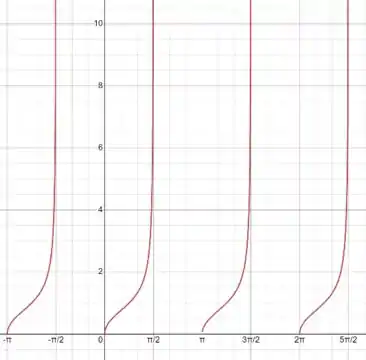
Nesse caso, quando a função volta a repetir seu desenho. Então:
Passo 4
Analisando o gráfico da função:
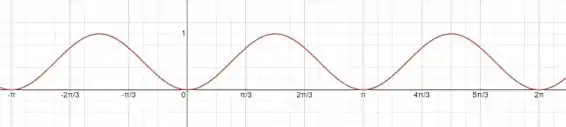
Como podemos ver, com a função volta a repetir seus valores. Logo:
Passo 5
Analisando o gráfico da função:
![]()
Nessa situação, a curva mantém sua oscilação, porém não repete o sei início. Logo, ela não é periódica!
Resposta
Compreendeu como analisar a periodicidade das funções?Qualquer dúvida que tiver, pode falar com a gente!