O gráfico de uma função diferenciável y = y(x) passa pelo ponto (0, 1) e em cada ponto P(x, y) do gráfico a reta tangente é perpendicular à reta que passa por P e pela origem. Encontre um problema de valor inicial cuja solução seja y(x).
Passo 1
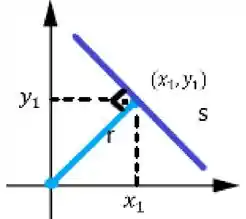
Para resolvermos essa questão, vamos utilizar a ideia base de retas. Olha só, a imagem abaixo demonstra exatamente o problema da questão, temos uma reta (r: azul claro) que sai da origem do plano cartesiano e passa pelo ponto P(x,y), nesse ponto P há uma reta perpendicular (s: azul escuro).
Passo 2
Até aqui tá beleza, né?
Continuando, sabendo que a reta “r” e “s” são perpendiculares, podemos considerar que o coeficiente angular é:
Sendo → coeficiente angular de r e → coeficiente angular de s
Passo 3
Ou seja, em relação aos coeficientes angulares podemos considerar:
Então:
Se substituirmos, temos que:
Reescrevendo