Passo 1
Fala, pessoal!!!
Inicialmente, nós queremos uma estimativa para essa equação dado .
Para , temos
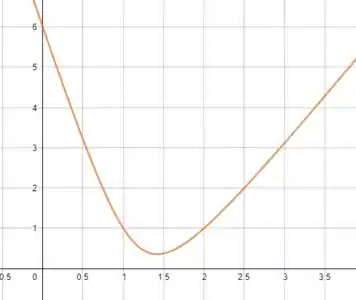
Bora identificar nossos pontos olhando para o gráfico!
Quando . Então, .
Quando . Então, .
Substituindo:
Passo 2
Repetindo o procedimento para , temos
Bora identificar nossos pontos olhando para o gráfico!
Quando . Então, .
Quando . Então, .
Substituindo:
Passo 3
Agora vamos responder a pergunta de milhõeeees:
Esses números são maiores ou menores que ?
Lembra da definição da derivada?
Substituindo
Como temos um e um , podemos dizer que tende para uma média desses dois valores, ou seja:
Assim, fica mais fácil visualizar que para a estimativa é , que é maior que . Para a estimativa é , que é menor que .
Resposta
Para a estimativa é , que é maior que .
Para a estimativa é , que é menor que .