Depois que uma massa pesando 10 libras é presa a uma mola de 5 pés, a mola passa a medir 7 pés de comprimento. A massa é então removida e substituída por outra de 8 libras. O sistema todo é posto então em um meio que uma força de amortecimento numericamente igual a velocidade instantânea.
- Encontre a equação do movimento supondo que a massa seja solta incialmente solta do ponto abaixo da posição de equilíbrio e a uma velocidade de 1 pé/s para baixo
- Expressa a equação do movimento na forma dada em (23)
- Ache o instante no qual a massa passa pela posição de equilíbrio dirigindo-se para baixo
- Faça ao gráfico do movimento.
Passo 1
Faaaala, cara! Tranquileba?
Temos que:
Temos emntão:
Façamos
Passo 2
Fazendo
Assim:
Lembrando:
Vemos logo que
Logo:
Fazendo
Passo 3
Assim:
Fazendo
P
ara: encontraremos os valores de A e B pelas condições iniciais. Veja:
- É dito que a massa é solta de um ponto pé abaixo da posição de equilíbrio, logo
- É também dito que a massa é solta com uma velocidade para baixo, logo
Assim:
Logo:
Lembrando
Resposta
- Será quando , o que implica
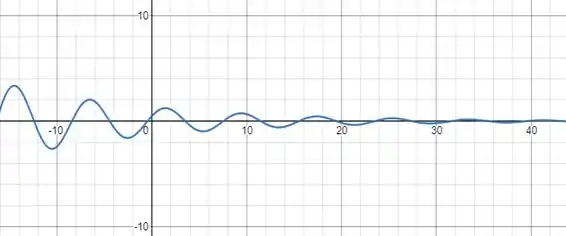
Veja que à medida que aumenta, a equação tende ao zero.