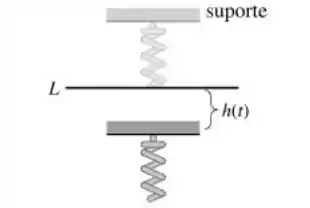
Uma massa é presa a uma mola cuja constante de elasticidade é Depois que a massa atinge a posição de equilíbrio, seu suporte começa a oscilar verticalmente me relação a uma linha horizontal L de acordo com uma formula . valor de representa a distancia em pés medida a começar de L. Veja a figura
- Qual é equação diferencial se todo o sistema move-se através de um meio que oferece uma força de amortecimento numericamente igual a
- Resolva equação diferencial do item a) admitindo que a mola é distendida em 4 pés por uma massa pesando 16 libras e
Passo 1
Faaaala, cara! Tranquileba?
Temos a seguinte EDO:
A EDO acima é caracterizada como de segunda ordem, não homogênea e de coeficientes constantes. EDO’s desse tipo tem como solução a soma de duas soluções chamadas de solução particular e solução homogênea Para nós, físicos, geralmente chamada de solução transiente/transitória ( e solução estacionária (
Passo 2
Para
Fazendo
Ficando:
Aqui temos tres casos:
- Subcrítico: Se
- Crítico: Se
- Supercrítico: Se
Casos em que dependem doa valores dados no item b) que veremos em breve.
Para
Façamos
Soluções de uma EDO desse tipo constitui um espaço vetorial de dimensão 2 que comportam infinitas soluções. Deste modo, façamos uma função parecida. Assim:
De modo que podemos formar uma função
Façamos
Ficando:
Ficando:
Que ainda constitui um valor que contem imaginário. Estamos resolvendo a equação para um problema real, logo não é normal haver uma parte imaginário. Para eliminá-lo, multipliquemos pelo seu conjugado:
Ficando:
Logo:
Logo:
Lembrando
Logo nós temos que descobrir sob qual regime de amortecimento o sistema está sujeito para resolver a solução
Passo 3
Para b) temos que:
Sabendo que logo
E dado que
Logo:
Caso supercrítico.
Logo:
Para acharmos os valores de
- É dito que é
- Também que
Que assim achamos os seus respectivos valores.
E para
Substituindo os valores
Resposta
Logo temos que: