Uma massa de 1 slug é presa a uma mola cuja constante é Inicialmente a massa parte de 1 pé abaixo da posição de equilíbrio a uma velocidade de para baixo e o movimento subsequente tem lugar em um meio que oferece uma força amortecedora igual a duas vezes a velocidade instantânea.
- Qual é a equação do movimento se a massa sofre a ação de uma força externa igual a
- Faça o gráfico das soluções transiente e estacionária no mesmo conjunto dos eixos coordenados
- Faça o gráfico da equação do movimento
Passo 1
Faaaala, cara! Tranquileba?
Sabemos que:
Logo nossa EDO fica:
Que pode escrita como:
Chamemos
Assim:
Passo 2
Sabemos que uma equação diferencial linear, não homogênea de coeficientes constantes e de segunda ordem, admite como solução geral é a soma da solução transiente com a solução estacionário Sendo, portanto
Para :
Fazendo
Assim:
Lembrando que: e dado esses valores, vemos que:
Façamos
Assim:
Fazendo
Para: encontraremos os valores de A e B pelas condições iniciais. Veja:
- É dito que a massa é solta de um ponto 1 pé abaixo da posição de equilíbrio, logo
- É também dito que a massa é solta com uma velocidade para baixo, logo
Assim:
Logo:
Lembrando que: e
Passo 3
Para
Soluções de uma EDO desse tipo constitui um espaço vetorial de dimensão 2 que comportam infinitas soluções. Deste modo, façamos uma função parecida. Assim:
De modo que podemos fazer uma função
Façamos
De modo que:
Que ainda constitui um valor que contem imaginário. Estamos resolvendo a equação para um problema real, logo não é normal haver uma parte imaginário. Para eliminá-lo, multipliquemos pelo seu conjugado:
Sabendo que
Portanto:
Lembrando que: e
Resposta
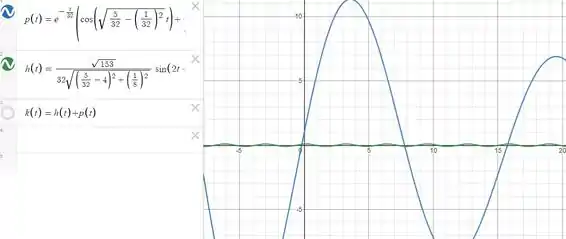
Onde a linha em verde é a solução estacionária, e a azul a transiente.
c)
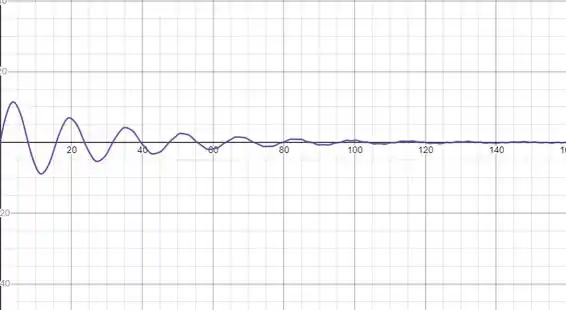
Perceba que após certo tempo a solução já não se altera mais, o porque disso é devido a solução mais geral dada no item a). Quando t fica muito grande, a solução transiente ( tende para o zero, de modo que a única que permanece e determina a posição é a solução estacionário por isso seu nome.