Medianas de um triângulo
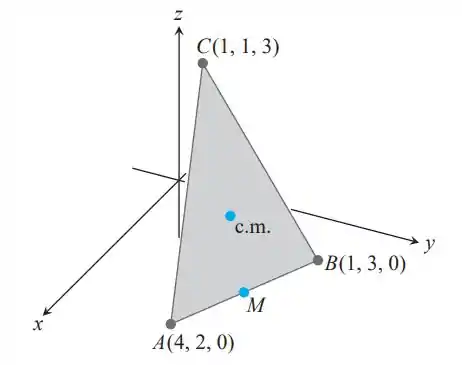
Suponha que A, B e C sejam os vértices da placa triangular fina de densidade constante mostrada a seguir.
- Encontre o vetor de C ao ponto médio M do lado AB.
- Encontre o vetor de C ao ponto que está localizado a dois terços do caminho entre C e M na mediana CM.
- Encontre as coordenadas do ponto no qual as medianas do ∆ABC se cruzam. De acordo com o Exercício 17, Seção 6.6, esse ponto é o centro de massa da placa.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de vetores e a geometria do espaço.
Vamos agora resolver os exercícios da seção 2 sobre teoria e aplicações de vetores e geometria espacial.
Item a
Analisando o enunciado, podemos calcular o ponto médio de AB:
E o vetor pedido:
Ou:
Item b
O vetor pedido é dado por:
Passo 2
Item c
Sabemos que o vetor cuja soma, é o vetor da origem até C e o resultado da parte (b) terminará no centro de massa. Logo, teremos:
Que é o ponto:
E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.