o método Adams-Bashforth/Adam-Moulton para:
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão ele pede para achar método de Adams-Bashforth/Adam-Moulton nos problemas.
Para
Lembrando que para essa questão temos que usar a fórmula do método Adams-Bashforth/Adam-Moulton em que,

Passo 2
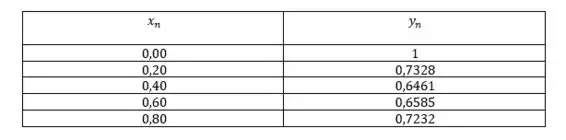
Utilizando este método vamos ter que,
Seguindo a sequência até ficamos com
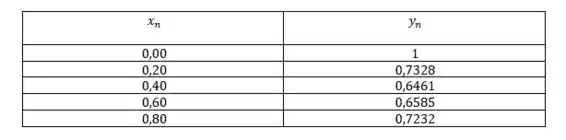
Ufa, complicadinha, mas é isso aí até a próxima

Resposta