A movimentação de um conjunto de partículas se movendo ao longo do eixo x é controlada pela equação diferencial
onde x(t) indica a posição da partícula no instante t.
(a)Se uma partícula estiver localizada em x = 1 quando t =2, qual é sua velocidade nesse instante?
(b) Mostre que a aceleração de uma partícula é dada por
(c) Se uma partícula está localizada em x = 2 quando t = 2,5, ela poderá alcançar o local x = 1 em qualquer momento posterior? [Dica: t³ − x³ = (t − x)(t² + xt + x²).]
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
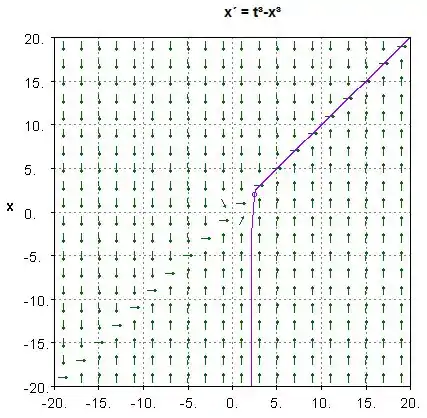
- Faça o gráfico do campo de direção da velocidade x′(t). Ao representar graficamente o valor inicial de x(2,5)=2, podemos ver mais visivelmente a tendência do campo. Não, a partícula se estabiliza em torno da velocidade de x′(t)=1. Isso implica que a posição da partícula está sempre aumentando e só pode atingir uma vez.
A velocidade x′(t) em qualquer ponto pode ser resolvida substituindo a posição x e o tempo t na EDO. Substitua o ponto x(2)=1 na EDO e resolva para x′(t).
Passo 2
Passo 3
Resposta
a) x'(t)=7
b) Diferenciando a equação dada em relação a t, obtemos o resultado desejado.
c) Não, porque a posição da partícula está sempre aumentando.