Passo 1
Fala, galerinhaaa!
Vamos começar achando os valores de que atendem a essa inequação, beleza?
Mão na massa!
Um pouco diferente de tudo que estudamos até aqui, né?
Bem, primeiro vamos resolver como se fosse uma equação do segundo grau, depois nos preocupamos com o , ok?
ou
Agora que vem o pulo do gato!
Nossa inequação é: , ou seja, queremos o intervalo no eixo onde a nossa função seja MENOR que ZERO. Vamos traçar um gráfico para visualizar:
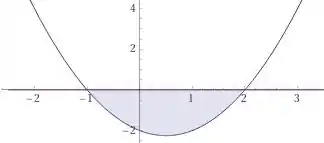
Perceba que na área pintada de azul a nossa função assume apenas valores negativos.
Logo, podemos dizer que:
Não colocamos o sinal de para não incluir os valores nulos da nossa função.
Show!!!
Passo 2
Agora vamos expressar a solução com a notação de intervalos e em seguida vamos representa-la na reta dos reais.
Bem, nossa solução deu que , certo?
Então você concorda que nossa restrição é para valores menores que e para valores maiores que ?
Concorda também que, como não aparece o sinal de em ambas as restrições tanto o quanto o não se incluem nos valores que podem ser assumidos por ?
Então beleza!
A nossa expressão em notação de intervalos fica assim:
E a nossa representação na reta dos reais fica:

Agora acabou! ;)