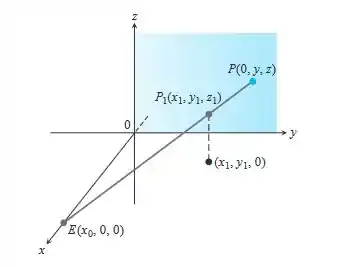
Perspectiva em computação gráfica - Em computação gráfica e desenho em perspectiva, precisamos representar objetos vistos pelo olho no espaço como imagens em um plano bidimensional. Suponha que o olho esteja em , conforme mostrado aqui, e que desejamos representar um ponto como um ponto no plano . Fazemos isso projetando no plano com um raio a partir de E. O ponto será representado como o ponto . O problema para nós, como designers gráficos, será encontrar e , dados e .
a. Escreva uma equação vetorial entre e que seja verdadeira. Utilize a equação para expressar y e z em termos de e .
b. Teste as fórmulas obtidas para y e z no item (a) investigando seu comportamento em e e vendo o que acontece quando . O que você encontra?
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A - A equação vetorial pode ser escrita como
Com isso, podemos parametrizar da seguinte forma
Portanto,
Igualando os componentes correspondentes
Isolando o termo
E com isso,
Passo 2
B – Colocando , nós temos
Com isso, obtemos que
Colocando , nós temos que é indefinido, com isso
Como a maior potência de no numerador é igual à correspondente no denominador e ambas têm o mesmo fator, o limite é igual a . Portanto, usando , nós temos