Na primeira lacuna, escolha entre converge ou diverge.
Como
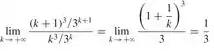
a série ![]()
__________ pelo teste __________.
Passo 1
Essa questão é extremamente fácil de resolver pelo fato de o comando já informar tudo que nós precisamos saber, acredita?
Olha só, o comando quer saber se a série é convergente ou divergente, para isso, podemos usar vários testes, para descobrir qual usar basta analisarmos as séries.
Se prestarmos atenção, temos:
1)
2)
Ou seja, o limite aplicado é o seguinte Teste da Razão, onde:
Passo 2
Portanto,
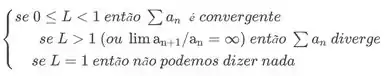
Sabendo que converge, e também são convergentes pelo teste da razão.