Na primeira lacuna, escolha entre converger ou divergir.
- A série
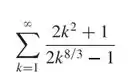
_______ por comparação com a série p dada por
![]()
Passo 1
Essa questão é extremamente fácil de resolver pelo fato de o comando já informar tudo que nós precisamos saber, acredita?
Olha só, o comando quer saber se a série é convergente ou divergente, para isso, podemos usar vários testes, nesse caso a própria questão já sugere o uso do teste de comparação.
Passo 2
Para o teste da Comparação temos de ter uma série “mais simples”, mas que tenha uma certa semelhança à série da questão, logo, concorda que podemos utilizar?
Sabendo que a série (1) diverge, a série dada na questão também diverge pelo teste da comparação.