No problema 9, calcule o coeficiente angular m da reta tangente ao gráfico de cada função no ponto indicado, esquematize o gráfico e mostre a reta tangente no ponto.
em
Passo 1
Podemos obter a inclinação da reta tangente, , de uma curva qualquer através da definição de derivada:
em que podemos identificar que o ponto indicado no enunciado , é construído da seguinte forma:
Passo 2
Temos então:
De forma que:
Passo 3
Expandindo o produto notável temos:
Simplificando os temos:
= 0
A reta tangente tem o seguinte formato:
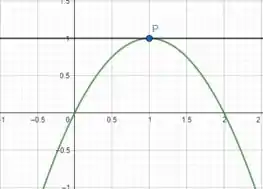
Resposta
Portanto:
O gráfico está ao final do Passo 3.