No problema 20, a conclusão do teorema do valor médio falha no intervalo indicado. Faça o gráfico da função e determine quais as hipóteses, do teorema do valor médio, que falham.
Passo 1
Oiiii, pronto para mais uma questão de cálculo?
Esse problema é bastante simples de se entender, bora lá? Primeiro vamos relembrar o que é o teorema do valor médio:
Se temos uma função que é bem definida e contínua em um intervalo fechado , assim como, diferenciável no intervalo aberto , então, para um valor qualquer, a reta tangente a esse ponto é paralela à uma reta que passe pelos pontos A e B.
Portanto, para resolver este problema, precisamos saber se a função é contínua e diferenciável, assim como fazer o gráfico da função.
Passo 2
Primeiro, o gráfico desta função pode ser esboçado jogando valores para no intervalo solicitado, você vai obter algo assim:
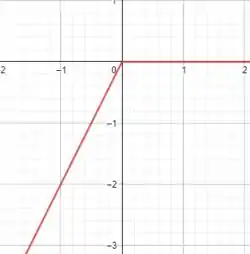
Pelo gráfico nós podemos notar que a função é contínua, no entanto, a quina em indica que esta função não é diferenciável em . Como este valor pertence ao nosso intervalo, o teorema falha nesta condição!
Resposta
Resposta ao longo do Passo 2.