Nos problemas 43-48, cada figura representa o gráfico da solução particular de uma dentre as equações diferenciais:
Passo 1
Faaaala, cara! Tranquileba?
Vamos achar o gráfico da solução particular do item a)
Temos então:
Façamos (transformações que não fazem diferença, mas nos ajudam a facilitar os cálculos)
Passo 2
Fazendo
Chamemos e
Passo 3
Logo temos a solução (chamemos a variável de x):
Lembrando de que
Logo: vemos que:
De modo que
Assim:
O gráfico da solução acima é desse tipo:
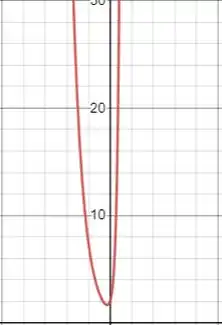
Que se assemelha ao gráfico da figura 4.3.3 do problema 44
Resposta
Que tem como gráfico a solução do problema 44.