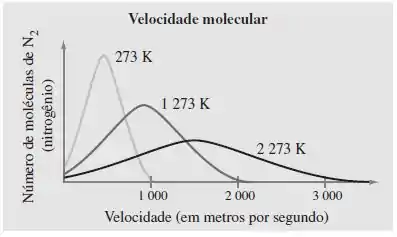
Química: velocidade molecular A figura mostra representações gráficas dos números relativos de moléculas de (nitrogênio) que têm uma dada velocidade em três temperaturas (em graus Kelvin). Identifique as diferenças nas velocidades médias (indicadas pelos picos das curvas) nas três temperaturas e descreva os intervalos nos quais a velocidade é crescente e decrescente para cada uma das três temperaturas. (Fonte: Adaptado de Zumdahl Chemistry, sétima edição.)
Passo 1
Nas três curvas, vemos que o gráfico das velocidades relativas é mais ou menos simétrico em relação ao pico das curvas. Então, sabendo aproximadamente a velocidade máxima – que é dada na calda final da curva – podemos estimar a velocidade média (nos picos das curvas) apenas dividindo a velocidade máxima por dois.
Para a temperatura , a velocidade máxima é . Dividindo esse valor por dois, obtemos a velocidade média como .
Para a temperatura 1, a velocidade máxima é . Dividindo esse valor por dois, obtemos a velocidade média como
Para a temperatura 2, a velocidade máxima é um pouco acima de . Mas é a melhor aproximação que temos a partir do gráfico. Então, dividindo esse valor por dois, obtemos a velocidade média como .
Nesse caso, vemos o seguinte padrão: quando aumentamos a temperatura em , a velocidade média das moléculas aumenta, aproximadamente, em .
Passo 2
Vemos que todas as curvas são crescentes até alcançarem a sua respectiva velocidade média e então se tornam decrescentes. Nesse sentido, podemos identificar os seguintes intervalos de crescimento e decrescimento.
Para a curva da temperatura , a velocidade cresce de a e decresce de a .
Para a curva da temperatura 1, a velocidade cresce de a e decresce de a .
Por último, mas não menos importante, para a temperatura 2, a velocidade cresce de a e decresce de a .
Resposta
Velocidades médias
:
:
:
Intervalos de crescimento e decrescimento:
: crescimento em e decrescimento em
: crescimento em e decrescimento em
: crescimento em e decrescimento em