Um recém-formado pegou emprestados R$ 100.000,00 a uma taxa de juros de 9% ao ano para comprar um apartamento. Prevendo constantes aumentos de salário, ele espera pagar a uma taxa mensal de 800(1 + t/120), onde t é o número de meses desde o início do empréstimo. a) Determine a quantia máxima que esse comprador pode financiar. b) Determine os juros totais pagos durante o financiamento.
Passo 1
No item a) deste exercício, podemos começar com o modelo do exemplo 2 da mesma seção. Neste modelo, o valor do investimento S(t) se relaciona com o valor r do juros e com o valor k pago por cada parcela, da seguinte forma:
onde, usando o valor de contorno que nos informa que temos um valor de investimento inicial, temos S(0) =
segue que . Para prosseguirmos, precisamos descobrir a taxa mensal, o problema é que temos apenas a taxa anual de 9%. Para resolver isso, vamos pensar da seguinte maneira: como estamos trabalhando com juros, cada mês temos uma nova aplicação dos juros, no caso de uma taxa anual a, cada mês contribuirá com e como estamos interessados apenas no valor da taxa (r), podemos escrevê-la da seguinte forma
onde o valor 1,09 aparece da aplicação da taxa de 9% (um aumento de 9% consiste numa multiplicação por 1,09) e a subtração por 1 pois queremos apenas o valor da taxa r.
Continuando, como o recém-formado pretende pagar com parcelas , temos que , pois o valor total da “divida” cai com o tempo. Segue que podemos escrever
como sabemos , basta procurarmos pelos valores que zeram essa equação acima. Vamos agora manipular um pouco, multiplicando os dois lados por
e passando alguns termos para a esquerda
e tudo que precisamos fazer agora é resolver a equação acima.
Passo 2
Infelizmente a equação que encontramos não pode ser resolvida de um modo analítico, nos resta apelar para os métodos numéricos, vamos imaginar então o encontro entre duas funções, uma f(t) e outra g(t), onde elas são
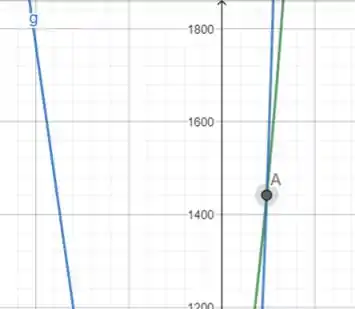

isso significa que o recém-formado precisa de 97 meses para terminar de pagar.
Passo 3
Para o item b), precisamos resolver S(t = 240) = 0
isolando
onde obtemos o valor .
Resposta
reais.