Um recipiente de água tem a forma dum cone circular reto com o vértice para baixo. A altura mede 10 pés e o raio da base 15 pés. A água sai pelo fundo à razão de c pés cúbicos por segundo. Calcular c de modo que o nível da água suba com velocidade de 4 pés por segundo no instante em que a profundidade da água é de 2 pés.
Passo 1
Bom, vamos começar essa questão já fazendo um desenho para nos auxiliar:
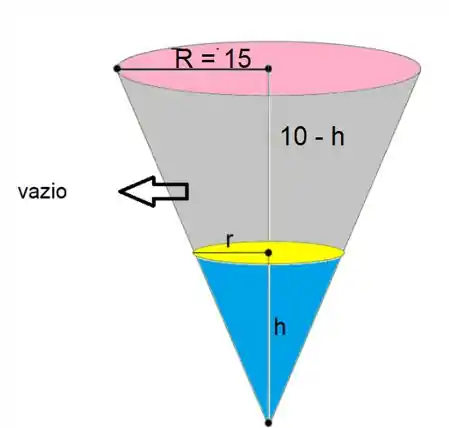
Agora vamos interpretar o que a questão nos passa.
Quando ela diz que a água sai pelo fundo à razão de 1 pé cúbico por segundo é equivalente a dizer que o volume varia de 1 pé cúbico por segundo, saindo por baixo, ou seja:
Então temos que a água sai a uma razão de 1 pé cúbico por segundo e entra numa razão de c pés cúbicos por segundo, e no final, queremos que a resultante dessa “entrada – saída” seja +4 pés cúbicos por segundo.
Passo 2
Traduzindo para o matematiques, o que queremos é:
Logo, queremos que
Então basta acharmos c que achamos o que queremos
Passo 3
Vamos usar semelhança para relacionar r e h:
Sabemos que o volume de água, para uma altura h e um raio r é:
Vamos usar