A região polar dentro do círculo e fora do círculo é uma região polar simples dada pelas desigualdades
______________ ______________ e _____________ ________________.
Passo 1
Olá galera! Para resolver esta questão precisamos encontrar dois intervalos: primeiro, o intervalo onde o raio varia e segundo, o intervalo onde o ângulo varia. É claro que o esboço desta região polar nos levará a encontrar os dois intervalos procurados. Segue o esboço desta região (os círculos determinados por e foram chamados de C1 e C2 respectivamente):
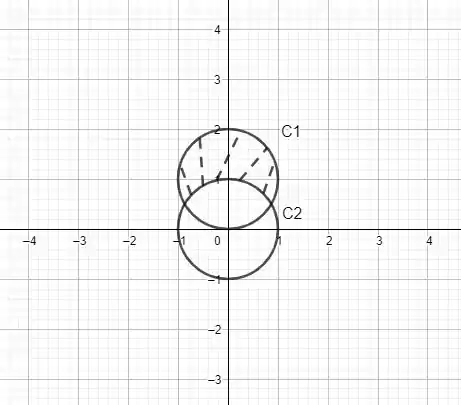
Passo 2
Viu que o esboço da região procurada, nos deu o intervalo onde o raio varia de cara? Pelo estudo desta seção, sabemos que na região tracejada o raio estará entre os raios dos círculos C2 e C1, e isto corresponde ao intervalo
Passo 3
Hufaaa, só nos resta agora encontrar o último intervalo. Repare que se o raio comece a varrer a região esboçada no sentido anti-horário, as duas curvas só irão se intersectar duas vezes, no primeiro e segundo quadrante. Sendo assim, a nossa tarefa é encontrar estes dois pontos de interseção em termos de ângulos. A melhor coisa a fazer é igualar as duas equações polares, isto é, igualando os seus raios.
Como as duas curvas se interceptam duas vezes (no 1º Quadrante e no 2º Quadrante), então as soluções são
e
Estas soluções nos mostram que o intervalo procurado é