Resolva a equação diferencial e, então, use um recurso computacional para gerar cinco curvas integrais para a equação.
Passo 1
Uma forma bem fácil de resolver essa questão é utilizar o método de Separação de Variáveis para obter uma equação e depois gerar possíveis curvas.
Logo, primeiro vamos colocar a equação no modelo: , sendo que cada termo deve ser dependente de apenas uma variável, ou seja, de um lado da equação tem apenas termos com “x” e no outro apenas com “y”, arrumando os termos, temos:
O próximo passo é integrar os dois lados da igualdade
→
Elevamos os dois lados da equação à função logarítmica para isolarmos o y:
Passo 2
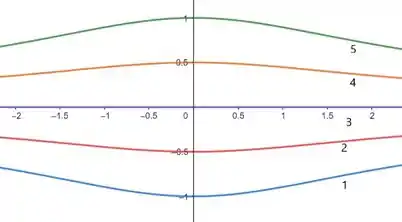
A partir da equação (1), podemos aplicar cinco possíveis valores positivos e negativos para “C” e obter diferentes curvas. A tabela a seguir mostra alguns valores típicos de “C”:

Passo 3
Depois disso, basta aplicar essas equações em um recurso computacional e obteremos as seguintes curvas
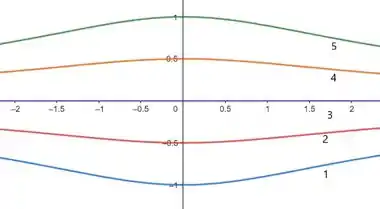
Resposta