Resolva a equação diferencial pelo método dos fatores integrantes.
.
Passo 1
O primeiro passo para resolvermos essa questão é lembrarmos o método dos fatores integrantes que exige que a equação esteja na forma:
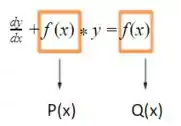
Assim, dividindo todos os termos por 2, temos:
.
A partir disso é possível determinar os coeficientes P(x)=2 e Q(x)= .
Passo 2
O segundo passo é determinar o fator integrante (u), sendo . Substituindo, temos:
→ .
Passo 3
E por último é só aplicar os valores obtidos na fórmula: . Portanto:
.
Resolvendo os termos semelhantes e aplicando a integral, temos:
.
Isolando o “y”:
.
Resposta