Resolva a inequação e represente a solução na reta numérica.
Passo 1
Uoooooooooooooooooou! Salve, salve! Vamos aqui resolver esse típico problema que é visto no 1º ano do Ensino Médio. Mas, aqui temos que ter um cuidado especial porque o segundo lado da desigualdade é zero e este tipo de problema pode ser bastante traiçoeiro porque a técnica do meio pelos extremos vai fazer com que fiquemos apenas com e a solução dessa equação só produz uma parte da resposta. Mais ainda, sem a análise da segunda equação, parte da resposta obtida com a primeira equação é considerada correta, sendo que não é. Vamos deixar isso mais claro quando fizermos a análise gráfica.
Passo 2
Vamos analisar a primeira inequação:
O domínio dessa inequação é dado por
Já a segunda inequação, , tem a solução
e o domínio é
Passo 3
Vamos fazer o estudo do sinal das duas inequações.
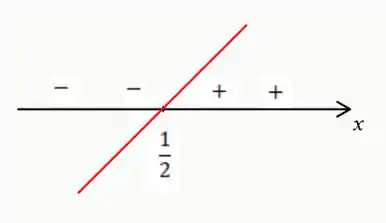
A primeira inequação é crescente, ou seja, a partir de os valores da inequação são positivos e abaixo são negativos. Isso pode ser representado na figura abaixo:
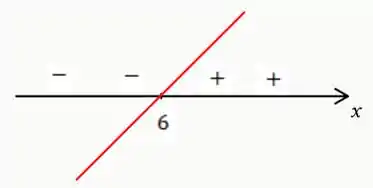
Já a segunda inequação também é crescete e o gráfico é semelhante ao primeiro. A diferença é o ponto onde :
Passo 4
Para fazermos a análise gráfica, vamos precisar de 3 retas. Uma para cada inequação e 1 para a combinação das duas. Como as 2 inequações já foram analisadas separadamente, só iremos estudar o sinal, então vamos colocar uma reta embaixo da outra mantendo um certo senso de proporção.
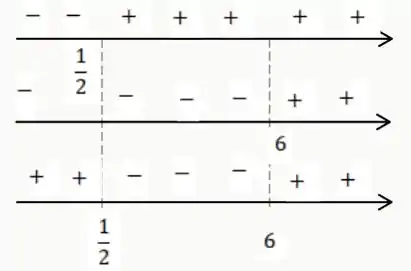
E aí está a configuração na terceira reta. Os valores negativos são os que estão entre e . Os valores positivos são os demais. Como a desigualdade não é inclusiva ( ou ), temos que o intervalo é do tipo “bola aberta”.
E assim, finalizamos mais uma questão. Vamos para a próxima?
Resposta
