Resolva a inequação e represente a solução na reta numérica.
Passo 1
Show de bola, galera! Vamos trabalhar uma questão de inequações com frações e já adianto que ela pode ser muito melindrosa porque o primeiro instinto de uma pessoa despreparada, que não é o nosso caso, é fazer “meio pelos extremos” e achar a resposta. Mas isso até um bom aluno do Ensino Médio sabe que é errado. Então, vamos apresentar a solução correta!
Passo 2
Agora, vamos ter que analisar cada inequação separadamente:
O gráfico dessa inequação é apresentado abaixo:
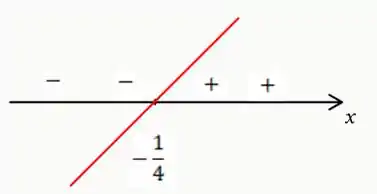
Para a segunda inequação, teremos
O gráfico dessa inequação também será apresentado abaixo:
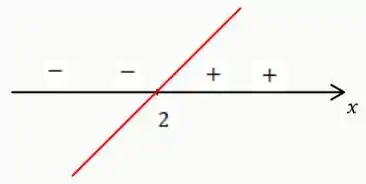
Passo 3
Para obtermos a resposta final, teremos que colocar 3 retas alinhadas e fazer o jogo de sinais. Eis a resposta:

Agora vamos analisar a inequação que resultou na resposta
Podemos ver, a partir dela, que queremos uma respota não positiva. Essa resposta será obtida onde o sinal é negativo. Assim, a resposta final, do tipo “bola fechada” porque se trata de uma desigualdade inclusiva, é

E assim, terminamos mais uma questão. Vamos pra próxima?
Resposta
