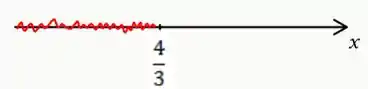
Resolva a inequação de valor absoluto e indique a solução na reta com números.
Passo 1
Show de bola, galera! Nesse tipo de problema vamos precisar analisar 2 situações. Uma quando o valor dentro do módulo for positivo e a outra quando for negativo. Assim, vamos começar.
Passo 2
situação:
A análise dessa inequação nos fornece que
e também
Juntando as duas soluções, obtemos
situação:
A análise dessa inequação nos fornece que
e também
Juntando as duas soluções, obtemos
Passo 3
A resposta final será a composição das 2 situações. Assim
que pode ser simplificada por
Como a questão está nos pedindo a resolução na reta, teremos
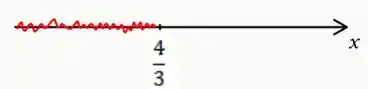
E assim, terminamos mais uma questão. Vamos para a próxima?
Resposta