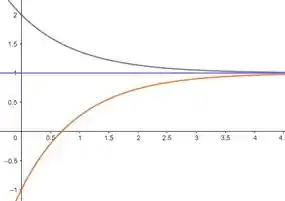
Resolva o problema de valor inicial no Exercício 3 e use um recurso gráfico computacional para confirmar que as curvas integrais dessas soluções estão de acordo com os esboços obtidos a partir do campo de direções.
Passo 1
Vamos resolver mais uma questão?
Para achar o valor inicial de uma equação temos é necessário colocar a equação no modelo: , sendo que cada termo deve ser dependente de apenas uma variável, ou seja, de um lado da equação tem apenas termos com “x” e no outro apenas com “y”, arrumando os termos, temos:
O próximo passo é integrar os dois lados da igualdade
Para retirar a função logarítmica do “y”, elevam-se os dois lados da equação à base “e”, assim:
Passo 2
O próximo passo é integrar os dois lados da igualdade
Para retirar a função logarítmica do “y”, elevam-se os dois lados da equação à base “e”, assim:
Passo 3
E por último aplicamos as condições iniciais na equação (1)
(a) y(0) = −1 (b) y(0) = 1 (c) y(0) = 2
a) y(0) = -1
b) y(0) = 1
c) y(0) = 2
Essas equações aplicadas em um recurso computacional geraram o seguinte gráfico que corresponde ao esboço obtido na questão anterior com o campo de direção.
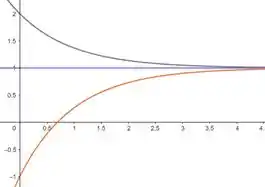
Resposta