Resolver graficamente os sistemas de equações:
- ;
- ;
- ;
- ;
- .
Passo 1
Temos:
Então:
Assim, atribuindo valores a e encontrando a imagem em , teremos o seguinte gráfico:
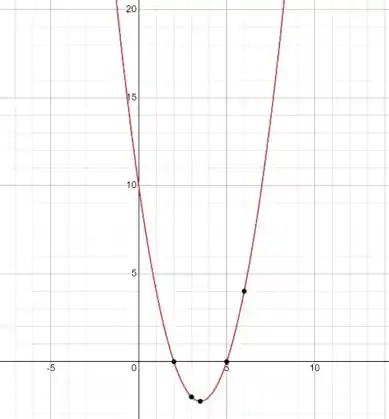
Passo 2
Temos:
Então:
Assim, atribuindo valores a e encontrando a imagem em , teremos o seguinte gráfico:
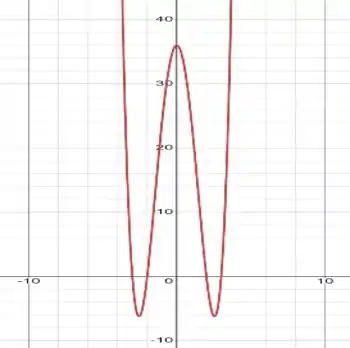
Passo 3
Temos:
Então:
Assim, atribuindo valores a e encontrando a imagem em , teremos o seguinte gráfico:
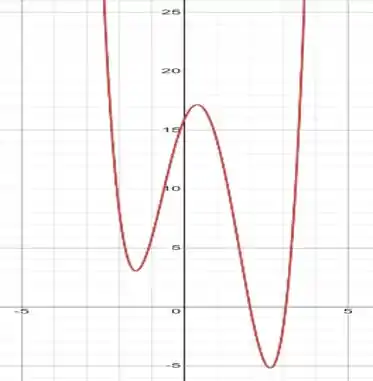
Passo 4
Temos:
Então:
Assim, atribuindo valores a e encontrando a imagem em , teremos o seguinte gráfico:
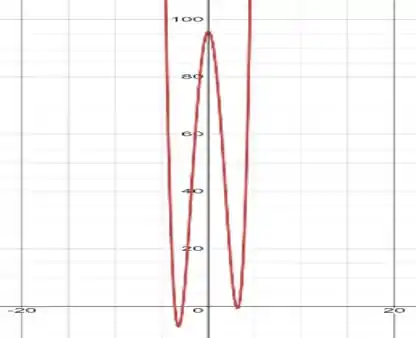
Passo 5
Temos então o seguinte gráfico:
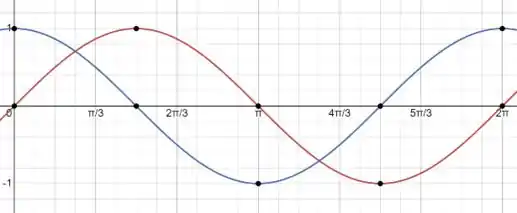
Resposta
Conseguiu esboçar as curvas aí?
Qualquer dúvida é só falar!