Um retângulo está crescendo de tal modo que, quando seu comprimento mede 5 cm e sua largura mede 2 cm, o comprimento está crescendo a uma taxa de 3 cm/s e a largura está crescendo a uma taxa de 4 cm/s. Nesse instante, a área do retângulo está crescendo a uma taxa de __________.
Passo 1
Bom, esse exercício exige um pouco mais de interpretação e imaginação, vamos lá!
Imaginamos um retângulo como o da figura abaixo.
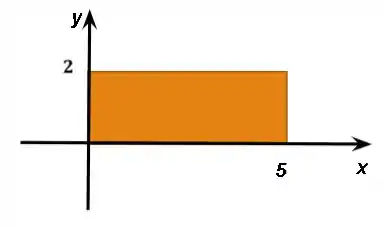
Considerando que, nesse ponto, ele continua crescendo a uma taxa de 3 cm/s de comprimento e de 4 cm/s de largura, que corresponde em termos numéricos a:
E lembrando que a área de um retângulo é calculada pela multiplicação dos seus lados, ou seja:
Temos agora todos os termos para utilizar a Regra da Cadeia para obter a taxa de crescimento da área desse retângulo.
Passo 2
Assim, temos:
Agora ficou tranquila, né?
Resposta
A área do retângulo está crescendo a uma taxa de 26 cm/s.