Sea .
- Probar que en toda recta que passe por (0,0) hay um intervalo que contiene en su interior a (0,0) que está em
- Se define por sin y si Para se define . Probar que cada es continua em 0, pero que f es no continua en (0,0)
Passo 1
Faaaaaala, galera... Tranquileba??
Para a)
Antes disso, façamos o gráfico das funções do conjunto dado, ou seja, a reta para que passa pelo (0,0), e a parábola para que passa pelo (0,0)
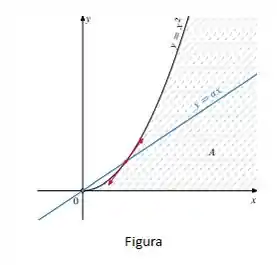
Veja que para toda a linha está em , de forma que a reta intercepta a meia parábola no ponto (0,0) em e mais nenhum outro lugar.
Passo 2
Para b)
Provamos no item a que a função f não é continua no ponto 0. Veja que sim, mas .
Para a continuidade da função num ponto, temso que provar que há um , para que assim exista satisfazendo
E com a=0, .
Maaaaas:
Agora, conforme dado, é continua em 0 para todo . Seja , então conforme dado , e então é contínua em 0, mas não para a função f.
Resposta
Ei, a resposta está no passo a passo :)