Seja com n inteiro positivo. Utilizar o teorema do binômio para desenvolver e a fórmula.
Exprimir a soma do segundo membro recorrendo ao símbolo somático. Faça-se e concluir derivado doutro modo no Exemplo 3
Passo 1
O nosso primeiríssimo passo é manjar desse tal de Teorema do Binômio, vamos relembrar? Bom, o teorema do binômio é uma equação que nos diz como uma expressão da forma se desenvolve para um número natural n, também nos permite saber, por um termo dado por a k b n-k, qual é o coeficiente que o acompanha.. Desenvolvendo a soma, temos que:
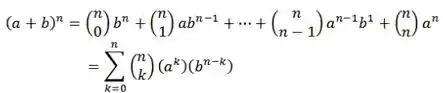
Passo 2
Belezinha, agora vamos usar esse teorema maroto, reescrevendo a função f(x) como a soma de duas funções, teremos:
Pera que a gente ainda não terminou, o enunciado pediu que provássemos a fórmula da soma de funções com o símbolo somático, logo:
Ou de uma forma diferente
Passo 3
Outro ponto da questão é aplicar o limite na função quando , o que será que acontece??