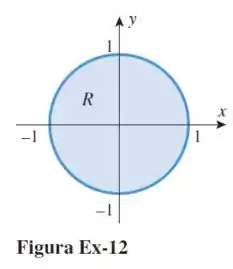
Seja a região dada na figura a seguir. Preencha as lacunas com os extremos de integração que faltam.
Passo 1
Fala galera! Essa questão consiste em analisar a figura e os limites da região .
Onde a coordenada vai de (-1,1) e a coordenada vai de (-1,1).
Passo 2
Letra (a) essa derivada dubla começa pela derivada em y e depois em x, assim temos:
Já na letra (b) a derivada dubla começa pela derivada em x e depois em y, assim temos: