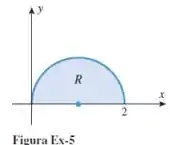
Seja R a região da figura a seguir. Preencha os limites de integração q ue faltam na integral
Em .
Passo 1
Bora galera iniciar mais uma questão!
Primeiramente vamos analisar a figura do exercício. Através dela podemos afirmar que o raio é igual a , essa informação nos ajuda a definir o limite em , assim temos que varia entre:
Passo 2
Agora vamos analisar em relação ao eixo x. Sabemos que x sempre é positivo e que:
Então, temos:
Para respeitarmos as coordenadas positivas e que temos:
Assim:
Temos: