Seja a região do primeiro quadrante delimitada pelos círculos e . Preencha as lacunas com os extremos de integração que faltam.
Passo 1
Observe aí galerada, o problema que nos foi proposto é seguinte: encontrar a região entre os círculos superior e inferior no primeiro quadrante e em seguida, encontrar os intervalos de variação do raio e ângulo. Os dois círculos dados e possuem raios respectivamente e e com centros na origem do sistema cartesiano XOY. Logo, o esboço da região de interesse é.
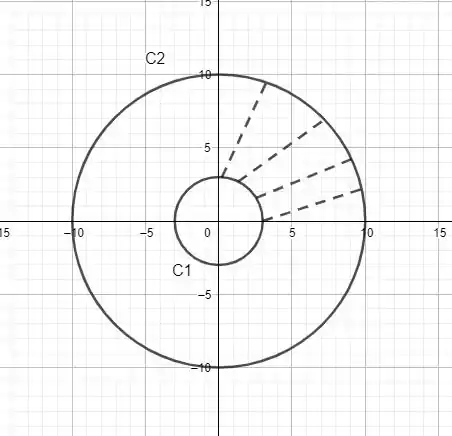
Passo 2
Dê uma olhada no esboço da região que esboçamos. Percebeu que a região procurada está entre os raios dos círculos C1 e C2, e sendo assim, podemos concluir que
Passo 3
Hufaa! Estamos terminando. Como a região procurada só preencheu o primeiro quadrante, então, podemos concluir que o intervalo procurado é