Seja C o segmento de reta de (0, 0) até (0, 1). Determine, em cada parte, a integral de linha ao longo de C por inspeção e explique seu raciocínio.
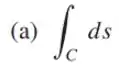
Passo 1
Oba, mais uma questão bem simples, vamos lá resolvê-la?
O primeiro passo é montar as equações paramétricas, para isso vale lembrar que uma reta tem o modelo:
r(t) = (x₀, y₀, z₀) + t(a, b ,c) (1)
Onde, (x₀, y₀, z₀) é um ponto qualquer pertencente a reta que liga A e B e (a, b , c) é o vetor diretor
O vetor diretor pode ser encontrado por: AB = B -A, podemos considerar A(0,0) e B(0,1)
AB = (0,1) - (0,0) = (0i ,1j)
Agora nós vamos escolher um ponto, A ou B, tanto faz, pegando o B(0,1) e aplicando a equação (1) da reta obtida anteriormente, temos:
r(t) = (0, 1) + t(0, 1)
r(t) = (1+t) j
Ou seja y(t) = 1+t e a sua derivada dy = 1
Passo 2
Olhando para a integral dada, é perceptível que ainda precisamos de alguns valores
Os limites de integração podem ser obtido substituindo na equação y(t) os valores que y varia, ou seja, ele vai de 0 para 1, assim temos:
0 = 1+t → t = -1
1= 1+t → t = 0
Passo 3
Por fim, vamos substituir esses valores na integral
Resposta
1