Seja o volume do sólido limitado acima pelo hemisfério e abaixo pelo disco compreendido pelo círculo . Expressando como uma integral dupla em coordenadas polares, ___________.
Passo 1
Gente para resolver esta questão precisamos esboçar a região que este raio gera. Isto pode ser feito dando os valores para a variável a partir de zero até onde a figura começará a repetir. Segue o esboço da região procurada:
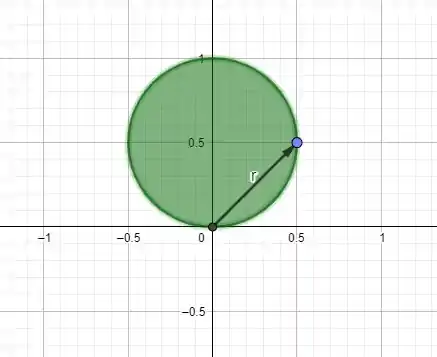
Passo 2
Mãos as obras! Note que a região esboçada foi gerada somente pelo o único raio, então teremos como intervalo para o raio o seguinte:
Passo 3
Que legal, já estamos no final da questão! Observe que se decidirmos varrer a região esboçada, o raio descreverá a mesma curva em intervalo de
Assim, podemos escrever