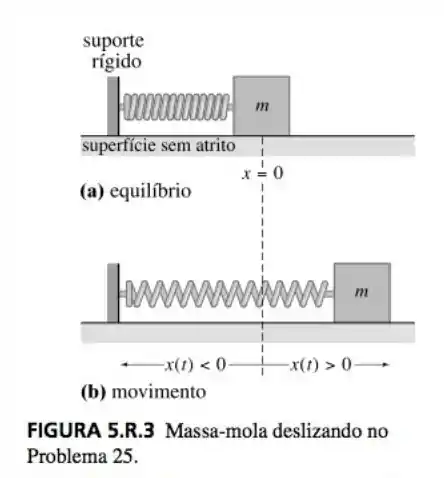
Suponha que uma massa deitada sobre uma superfície plana seca sem atrito, está ligada à extremidade livre de uma mola cuja constante é . Na figura 5.3.R(a) a massa é mostrada na posição de equilíbrio , isto é, a mola não está comprimida nem esticada. Conforme mostrado na figura 5.3.R(b) o deslocamento da massa para a direita da posição de equilíbrio é positivo e negativo para esquerda. Derive uma equação diferencial para o deslocamento da massa deslizante livremente. Discuta a diferença entre a derivação desta ED e a analise levando a (1) da seção 5.1
Passo 1
Faaaala, cara! Tranquileba?
Temos que a força de uma mola é do tipo:
Ou seja, se puxamos a massa para a esquerda, a mola faz uma força contrária. O análogo também é valido para movimento para a direita.
Passo 2
Assim dito, temos que:
Passo 3
Sabendo que
Esta ocorre em uma superfície horizontal, enquanto a equação (1) da seção 5.1, acontece com um sistema na vertical.