4. Suponha que e , , sejam soluções da equação
Onde e são supostas contínuas em . Suponha que o wronskiano de e não se anule em . Sejam , com e no intervalo , dois zeros consecutivos de , isto é, , e, para todo em , . Prove que existe em tal que . Interprete.
Sugestão: , segue que e . Verifique que e conclua que e têm sinais contrários.
Passo 1
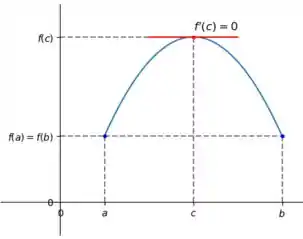
Bem, de acordo com o teorema do valor médio, para uma função contínua que zera duas vezes seguida em e , tem que existir um no meio deles tal que:
Só que no nosso caso :
Perceba que a função necessariamente deve crescer de um lado e decrescer de outro para isso ser verdade. Isso significa que em e , as derivas devem ter sentidos opostos. Logo...
Passo 2
O Wronskiano é uma função que não pode ser em nenhum ponto do intervalo onde a EDO está definida (intervalo ).
Isso significa que se ao calcularmos, a gente perceber que ele é positivo para um qualquer, então ele deve continuar positivo sempre, afinal para passar para os negativos ele tem que passar pelo :
Ou, se ele for negativo para , então ele deverá ser sempre negativo:
Como sabemos da sugestão...
Então, para não alterar o sinal do Wronskiano, Já que e , tem sinais opostos, então e também devem ter!
Assim, por exemplo, se for positivo e o wronskiano também, deve ser positivo. Como vai ser o oposto de (negativo), deve ser o oposto do , ou seja, negativo, saca?
Bem, se e tem sinais contrários, o só pode passar por em algum ponto entre eles (ponto que pode não ser o memso ponto do passo 1):
Resposta
Questão de demonstração.