O terceiro polinômio de Taylor de em torno de x = −1 é
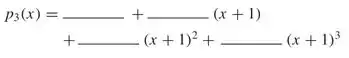
Passo 1
Acredita que é possível resolver essa questão de um jeito bem simples?
Olha só, primeiro nós vamos relembrar que os Polinômios de Taylor seguem o seguinte modelo:
Passo 2
E por fim, considerando as informações do comando da questão, temos que:
Substituindo esses valores na equação (1), temos: