Traçar o gráfico do polinómio , relativo ao intervalo . Determinar as constantes e de modo que a reta seja tangente à curva de no ponto . Uma segunda reta que passa por é também tangente ao gráfico de no ponto . Determinar as coordenadas e .
Passo 1
Faala aí? Para além do esboço do gráfico do polinómio, o exercício se resume em encontrar a equação da reta tangente ao gráfico onde a inclinação desta reta é igual a derivada da função neste ponto da abcissa. Na tentativa de encontrar a equação da reta tangente ao gráfico encontraremos cada incógnita pedida.
Passo 2
Esboço do gráfico do polinómio
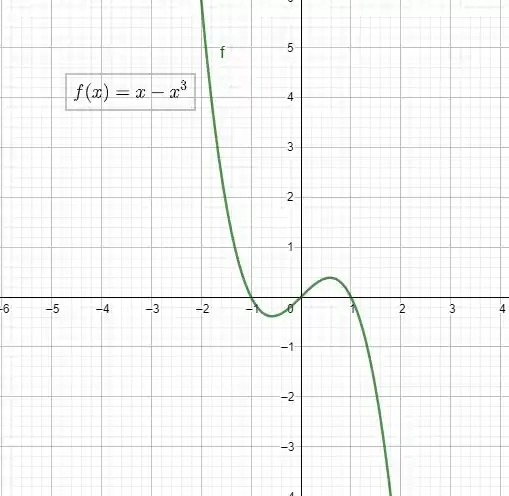
Passo 3
Como a reta é a reta tangente a curva no ponto , então
Logo,
Fazendo , teremos
Como a reta tangente a curva passa pelo ponto e tem inclinação , então podemos substituir estes pontos na equação da reta dada.
Passo 4
Usando o resultado do passo anterior, teremos
Logo, a equação desta reta é
Substituindo os valores das coordenadas dos pontos que passam pela reta e , teremos
Substituindo o segundo ponto, teremos
Como , e estão todas em função do , então
Substituindo novamente as coordenadas do ponto na equação desta reta, teremos