Um triângulo retângulo variável ABC no plano XOY tem o ângulo reto no vértice B, o vértice A fixo na origem e o terceiro vértice C obrigado a permanecer sobre a parábola . O ponto B parte do ponto no instante t = 0 e desloca-se no positivo
Com uma velocidade constante de 2 . Com que rapidez varia a área do triângulo quando t = 7/2 segundo?
Passo 1
Para começar vamos desenhar mais ou menos o que está ocorrendo
O gráfico é do tipo:
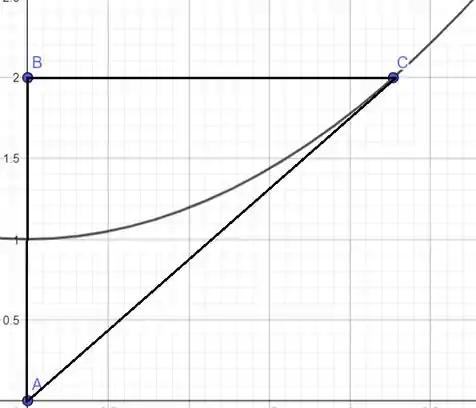
Nosso ponto B e C devem subir juntos (velocidade em y igual), pois B tem o ângulo (se um ficar com a coordenada y maior que o outro, não terá ângulo reto).
Sabemos pelo enunciado:
Passo 2
Fica evidente que iremos usar área e sua derivada (pergunta da questão), então vamos logo achar esses valores:
Ou seja, olhando essa fórmula fica claro que para achar a derivada da área temos que achar
Passo 3
Pela equação da parábola:
Sabemos pela física que:
Iremos achar isso para acharmos qual o valor de y, após
Olhando o movimento em y e usando que ele começa em :
Quando y = 8, temos x = 6 (basta ver a equação da parábola)Então, usando porém para
Resposta
A área varia com rapidez de