Use o campo de direções no Exercício 3 para fazer uma conjectura sobre o comportamento das soluções de y’ = 1 − y cuando x →+∞ e confirme sua conjectura examinando a solução geral da equação.
Passo 1
Fala galera, essa questão é moleza de entender, acredita?
De tão fácil, nós vamos resolver só olhando o campo de direções fornecido no exercício 3.
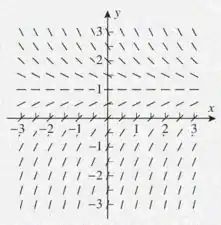
Passo 2
Analisando o campo de direções nós podemos fazer duas observações:
- O limite da equação é 1, pois é onde há a solução de equilíbrio, ou seja, o ângulo de inclinação é zero
- À medida que x → +∞ a tendência da curva é se afasta do ponto de equilíbrio.