Use uma integral dupla em coordenadas polares para calcular a área da região descrita: a região compreendida pela rosácea .
Passo 1
Olá galera! Lembrem-se que os problemas deste tipo se resolvem aplicando a seguinte fórmula
onde é a área duma região do plano xy.
Passo 2
Sendo assim, só nos resta esboçar a região com a finalidade de conhecer os intervalos onde e varia. Boraaa encontrar esses intervalos!
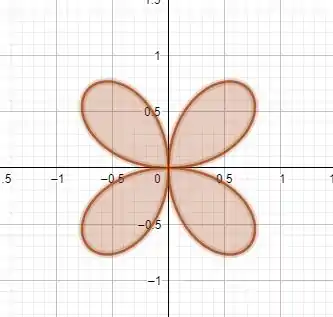
Olhando o esboço da região podemos notar que e . Galeraaa que tal aproveitar a simetria da região e integrando em e depois multiplicar esta integral pelo . É isso mesmo que iremos fazer!