Use o método de Euler com para aproximar a solução ao problema de valor inicial
No intervalo . Compare essas aproximações com a solução real (verifique!) representando um gráfico a aproximação de linha poligonal e a solução real no mesmo sistema de coordenadas.
Passo 1
Falaaa, meu querido/minha querida!! Para resolvermos essa questão, temos a seguinte fórmula.
Onde, e são os pontos iniciais dados pelo enunciado. E é definido por:
Bora para o exemplo!!!
Passo 2
A equação do enunciado é:
Então, e .
O enunciado nos diz que . Então, bora aproximar a solução.
Seguindo o processo, encontramos os valores:
A solução para a EDO o enunciado nos diz que é . Comparando os gráficos:
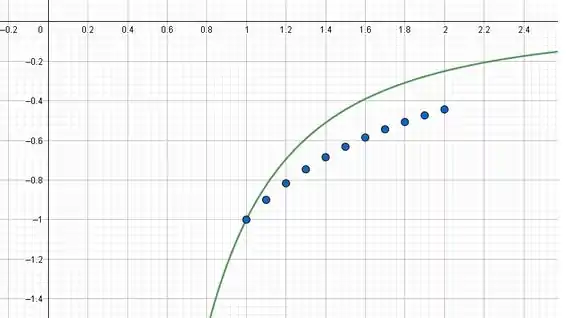
Resposta
Resolução nos passos anteriores.